The Math Behind Depth of Field
Following up on my recent article about depth of field, I really wanted to know how depth of field was calculated, so I read up on the math behind the phenomenon. Wikipedia’s article on depth of field has a lot of useful information about the math, and it goes into much more detail on it than I will here. Another great resource is The Manual of Photography by Allen & Triantaphillidou (Google Books link).
In this article, I walk through the math and visualize it to understand how it works. To start, I’ll define the important terms relevant to depth of field before introducing the equations that describe it. Lastly, I’ve created a calculator available on this site that lets you find the depth of field based on your camera settings.
Definitions
Depth of field is determined by four different variables: focal length, focus distance, the f-number, and the acceptable circle of confusion. Focal length is how zoomed in your lens is—a longer focal length is more zoomed in. Focus distance is just how far away your subject is. The f-number, which I discussed in my recent article on this subject, is a ratio between the focal length and the aperture diameter. Lastly, the acceptable circle of confusion is the amount of fuzziness we accept in an image before we start to think it looks out of focus. I’ll go through each of these in greater detail below.
A diagram showing the effect of aperture on blur and depth of field. Copyright BenFrantzDale - Diaphragm.svg, CC BY-SA 3.0, (Wikimedia link)
Another important term in the math behind depth of field is called circle of confusion. The circle of confusion describes how far light from a lens spreads out by the time it gets to the camera sensor. Someone decided to give this a confusing name, but a simple way to think about it is a “blur spot.” Numerically, it’s the diameter of this spot. The size of the spot determines the amount of focus blur, often called bokeh.
The circle of confusion is tiny. A theoretically perfectly in-focus image would have a circle of confusion of zero, but commonly accepted values fall between 0.029 mm and 0.035 mm, according to Wikipedia. The larger the circle is, the blurrier the photo is.
The f-number is the ratio between the focal length and the diameter of the aperture, . The depth of field increases with the f-number, as we’ll see with the math in the next section.
The formulas
The depth of field isn’t as wide in front of the subject as it is behind the subject. The two formulas for the near and far extent of this field vary only slightly. In the following formulas, and are the near and far limits of the depth of field, respectively. Next, is the focus distance, is the focal length of the lens, is the f-number, and is the acceptable circle of confusion.
The total depth of field is . But how does each variable affect it? In my last article, I already showed that the depth of field increases in proportion to the f-number . We can confirm that with these equations. For , as increases, the denominator gets closer and closer to zero, meaning depth of field reaches towards infinity. The graphs below provide a visual demonstration of how each variable affects depth of field.
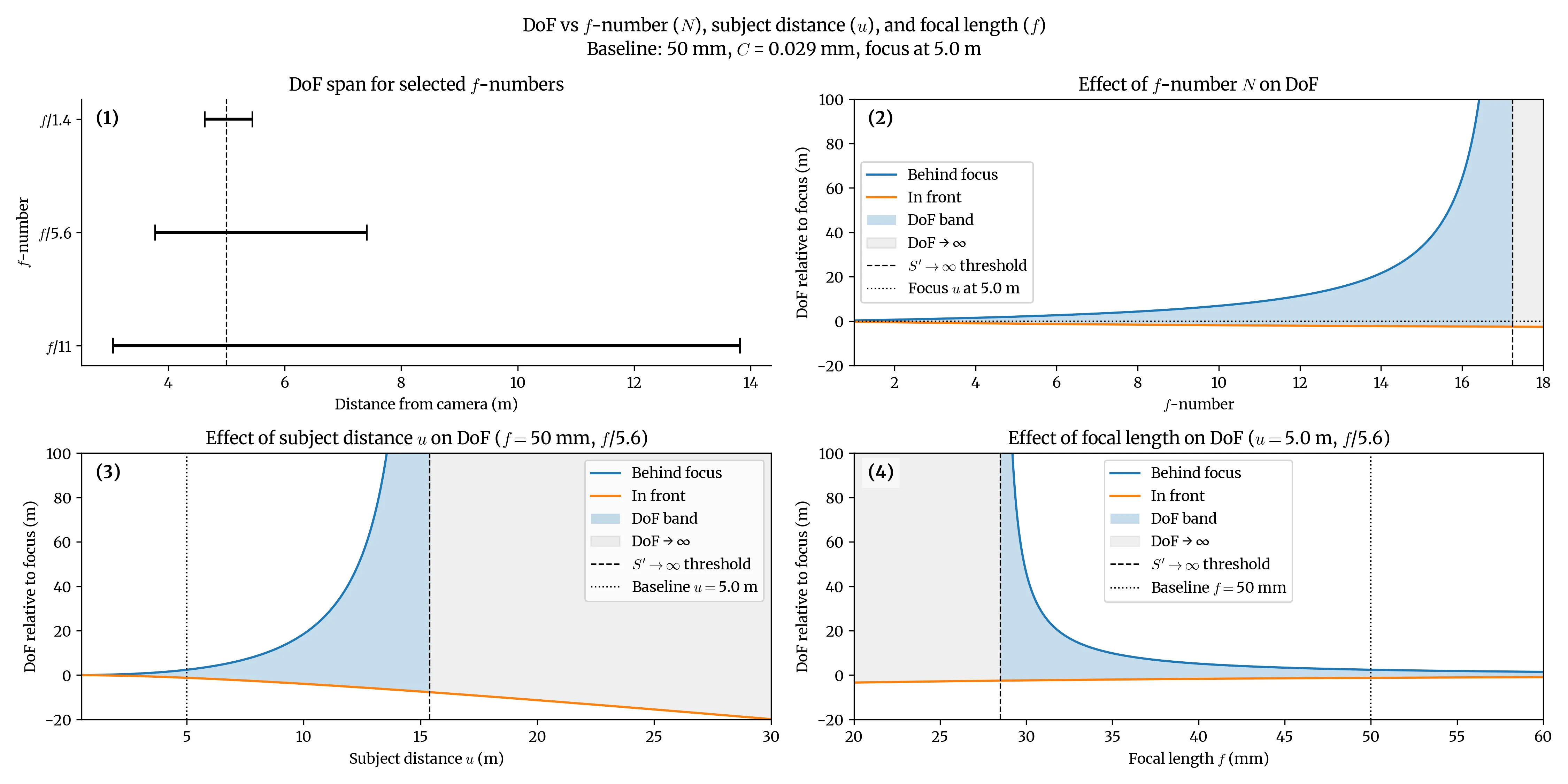
Graph 1 shows depth of field at various f-numbers; graphs 2–4 demonstrate how depth of field changes with each variable.
Graph 1 above shows the depth of field for different f-numbers. Graphs 2–4 show the threshold for infinite depth of field for the f-number, subject distance (same as focus distance), and focal length. The graphs clearly demonstrate how both the f-number and subject/focus distance are proportional to depth of field, while the focal length is inversely proportional. In other words, if you want a wider depth of field, increase the f-number, get farther away from your subject, or lower the focal length (i.e. zoom out).
Beyond here lies infinity
The focus distance after which the depth of field stretches to infinity is called the hyperfocal distance. This hyperfocal distance is shown in the graphs above as the threshold line on graphs 2-4. In mathematical terms, it looks like this:
For a focal length of 50 mm, an f-number of 8, and C as 0.029, the hyperfocal distance is about 10.77m. What this means is that for these camera settings, if you focus on a subject 10.77 m away, the depth of field will stretch behind the subject all the way to the horizon. The equation also shows how focal length and f-number affect the hyperfocal distance.
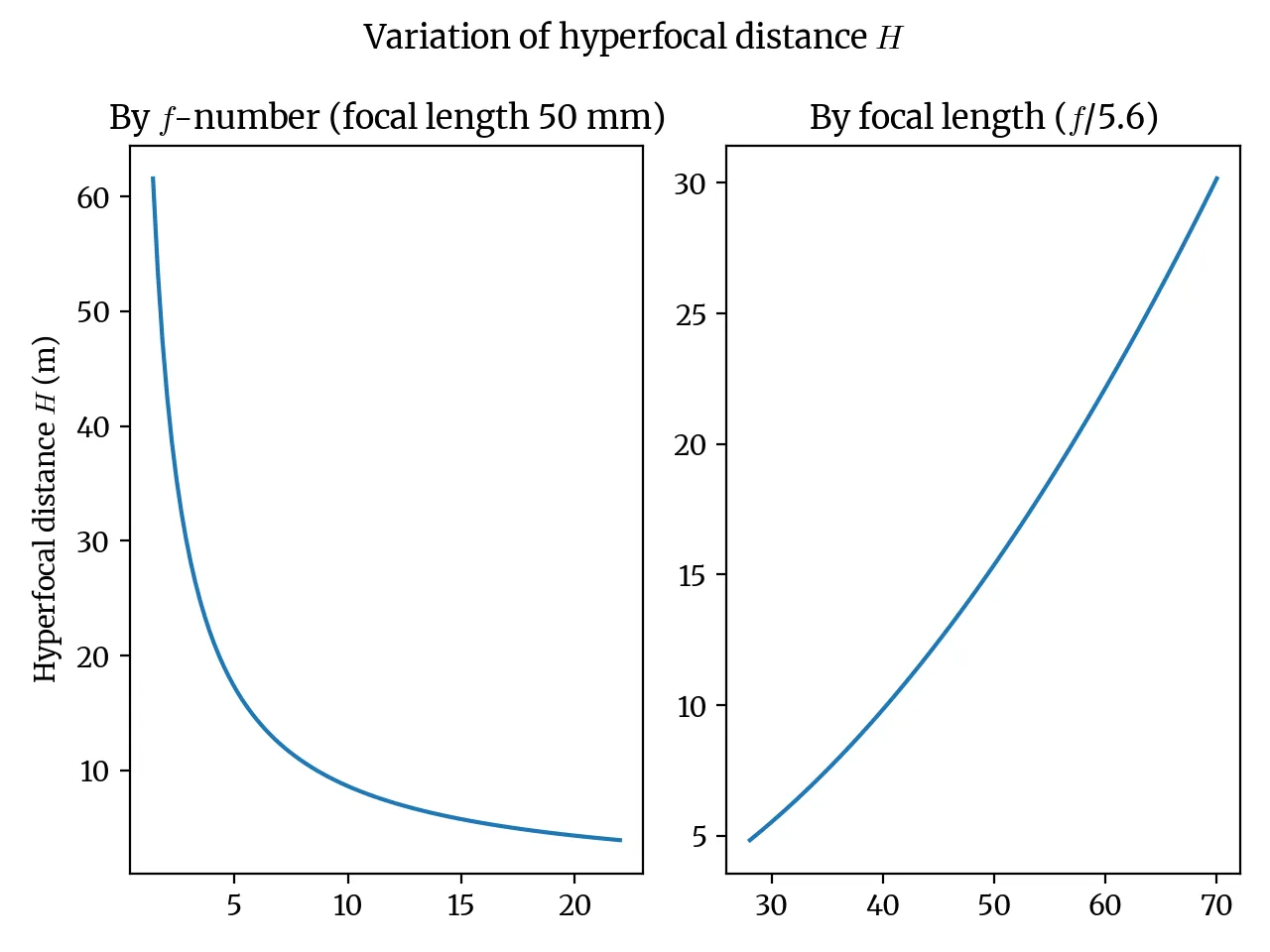
This can be especially helpful to landscape photographers, who typically want a wide depth of field to capture the detail of things both near and far. For example, we can use the graph to find an appropriate focus distance for our 50 mm lens at /8—approximately 10 m away.
Takeaways
I now have a better understanding of the math behind depth of field. Through the visualizations, I learned how each variable affects it, and satisfied my desire to know the numerical limits of depth of field for a particular case.
This math is too cumbersome to calculate offhand, but I’ve created a simple calculator that does the math for you based on your camera settings. You can play around with that at this link.